【AtCoder】ABC 340 C - Divide and Divide | 茶コーダーが解くAtCoder

atcoder.jp

実行時間制限: 2 sec / メモリ制限: 1024 MB / Difficulty: 528

問題概要

黒板に整数 が1個書いてあり、黒板に書かれている2以上の整数が全て無くなるまで以下の一連の操作を繰り返す。操作を行えなくなった時点で払った金額の総和は何円かを求めよ。

• 操作

1. 黒板に書かれている2以上の整数を1つ選び とする。
2. 黒板から を1個消し、新たに2個の整数 を黒板に書く。
3. 円払う。

制約

• 

考察

まずは小さい数字で実験してみよう。 のときの図を以下に示す。

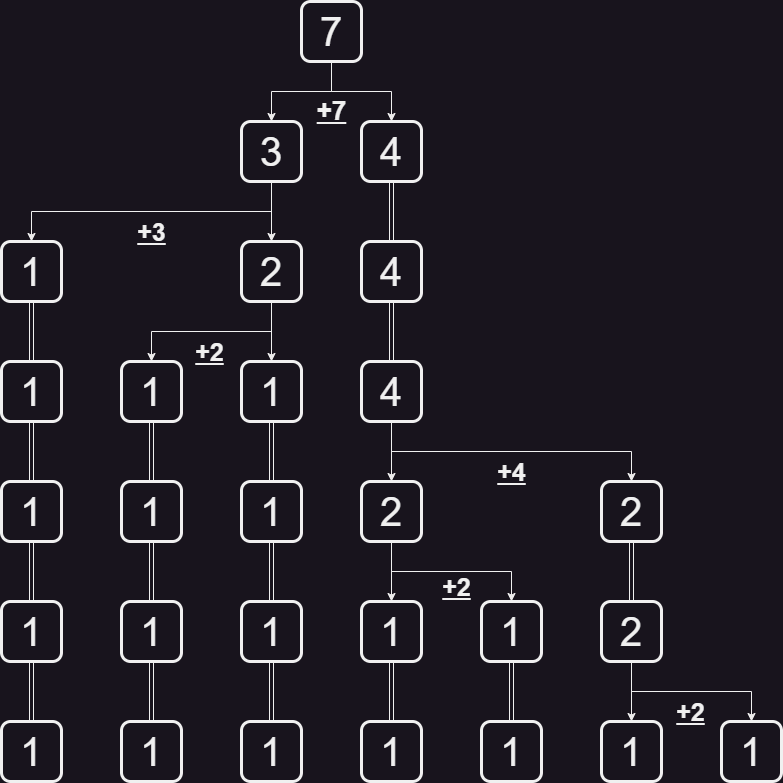
図を見てみると、「2 → 1」への遷移が何度も繰り返されていることが分かる。また、 のときに限らず であれば、どこかで「7」が出現した段階で、それ以降の遷移は上図と全く同じ遷移となる。つまり、「 から生成された数が全て になるまでに払う金額の総和」を とすれば、再帰的に以下のように書ける。

ただし、これを再帰関数としてそのまま実装すると TLE になってしまう。どこが時間の無駄になっているのだろうか。

それは、「同じ値の計算を何度も繰り返している」点にある。先ほどは の遷移の様子を図に書いてみたが、これが の場合であったらどうだろうか。1回目の操作後に黒板に書かれている数字は 「」が2つであり、定義式から

となる。ここで を2回呼び出す必要はない。なぜなら、1回目の計算で の結果は分かっているからである。

したがって、 の計算結果をあらかじめどこかに保存しておき、2回目以降の呼び出しはそれを参照すればよいのである。いわゆる「メモ化再帰」というテクニックだ。

メモ化再帰における「メモ」としては連想配列 ( C++ ではmap) を用い、keyを 、valueを とする。 f(x)が呼び出されたときには、map[x]が未登録ならば実際にf(x)を計算してreturnし、そうでないときはmap[x]をreturnすればよい。 のときに1をreturnさせるのを忘れないこと。

コード

#include <bits/stdc++.h>
using namespace std;

#define rep(i, start, end) for (ll i = (start); i < (ll)(end); i++)

ll ceil(ll a, ll b)
{
    if (a < 0 && b > 0)
        return a / b;
    if (a % b == 0)
        return a / b;
    return (a / b) + 1;
}

// ======================================== //

map<ll, ll> mp;

ll f(ll x)
{
    if (x == 1)
        return 0;

    if (mp[x] != 0)
        return mp[x];

    ll res = f(x / 2) + f(ceil(x, 2)) + x;
    mp[x] = res;
    return res;
}

int main()
{
    ll N;
    cin >> N;

    ll ans = f(N);

    cout << ans << endl;
}

atcoder.jp

実装時間: 15分